Filtres du premier ordre (1)
Introduction
Qu'est-ce qu'un filtre ?
De même qu'un filtre optique ne laisse passer que certaines couleurs, un filtre en électrocinétique ne laissera passer que certains signaux sinusoïdaux caractérisés par une pulsation .
A l'entrée du filtre, on applique par exemple une tension de pulsation ; si, à la sortie du filtre, la tension n'est pas trop atténuée, on considère que le filtre laisse passer la pulsation ; si au contraire, la tension est très atténuée, on considère que le filtre ne laisse pas passer la pulsation .
Le filtre sera alors caractérisé par l'ensemble des pulsations ou
fréquences qu'il laisse passer appelé bande passante.
Un filtre passe bas laisse passer les pulsations inférieures à une pulsation .
Un filtre passe haut laisse passer les pulsations supérieures à une pulsation .
Un filtre passe bande laisse passer les pulsations comprises entre et .
Un filtre coupe bande ou réjecteur de bande laisse passer les pulsations inférieures à et supérieures à
.
Un filtre peut donc être utilisé pour ne sélectionner que certaines pulsations (radio, TV...).
D'une manière générale, comme tout signal périodique peut-être considéré comme une superposition de signaux sinusoïdaux, connaissant le spectre du signal d'entrée et les caractéristiques du filtres, on peut en déduire le spectre du signal de sortie et donc la forme du signal après passage dans le filtre.
Filtre passe-bas du premier ordre
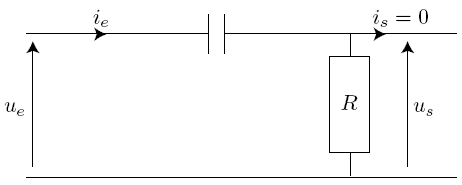
Comportement asymptotique
L'impédance du condensateur vaut
Si alors (refaire le schéma en supprimant la branche contenant le condensateur) et .
Si alors (refaire le schéma en remplaçant la branche contenant le condensateur par un fil) et .
On peut donc déjà dire que le filtre transmet les signaux de basse fréquence et atténue ceux de haute fréquence d'où la dénomination de filtre passe-bas.
Fonction de transfert
La fonction de transfert est définie par
en posant
Diagramme de Bode - Pulsation de coupure à -3dB
Représentation de la courbe de gain
Le module de la fonction de transfert est appelé gain
expérimentalement (oscilloscope ou multimètre)
On définie le gain en décibel
On représente le gain en décibel non pas en fonction de (ou ou ) mais en fonction de (la plage de fréquence pouvant s'étendre de quelques à et plus)
Si petit devant alors
Si grand devant alors droite de pente par décade ce qui signifie que si est multiplié par 10, augmente de 1 et diminue de
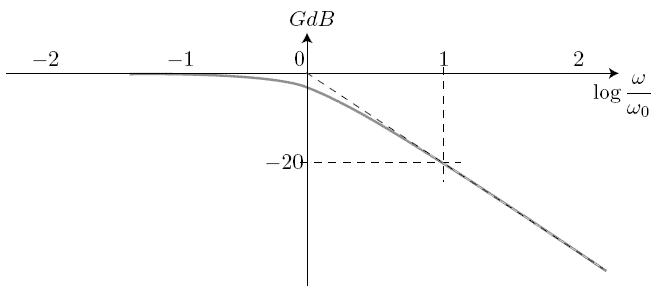
Les deux asymptotes se coupent pour c'est à dire pour ;
pour , et . est appelé pulsation de coupure à et noté .
La pulsation de coupure à du filtre est par définition la pulsation telle que
Elle peut être interprétée comme la limite entre les comportements BF et HF du filtre :
les signaux de pulsations sont transmis en sortie avec une atténuation inférieure à ;
les signaux de pulsations sont transmis en sortie avec une atténuation supérieure à ;
Idéalement on considérera que le filtre laisse passer une pulsation si l'atténuation en sortie est inférieure à .
La bande passante de ce filtre, c'est à dire l'ensemble des pulsations qu'il laisse passer, est donc .
Représentation de la courbe de phase
L'argument de la fonction de transfert est appelé phase
expérimentalement (oscilloscope)
On représente la phase non pas en fonction de (ou ou ) mais en fonction de (la plage de fréquence pouvant s'étendre de quelques à et plus)
Si petit devant alors
Si grand devant alors
Si alors
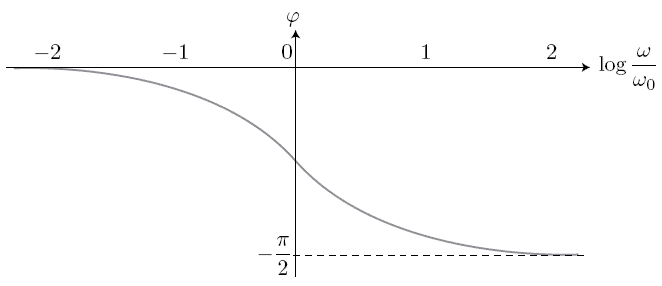
Pour ,
Pour ,
L'essentiel de la rotation de phase se fait donc entre
et c'est à dire sur deux décades.