Dynamique du point matériel (2)

---

Les vecteurs sont notés en gras.

Forces

Force de pesanteur - Chute libre

Soit un projectile de masse $m$ lancé avec une vitesse initiale ${\mathbf{v}}_0$ et soumis uniquement à son poids.

Système étudié : projectile de masse $m$ assimilable à un point.

Référentiel : référentiel d'observation (terrestre) supposé galiléen.

Bilan des forces : le poids $\mathbf{P}=m\mathbf{g}$

PFD : $m\mathbf{a}=m\mathbf{g}$

Projection : il s'agit de choisir le paramétrage le plus approprié au problème; les coordonnées cartésiennes avec un axe colinéaire à $\mathbf{g}$ sont, pour la chute libre, les plus appropriées.

$$\left\{\begin{array}{l}{a}_x=0\\ a_y=0\\ a_z=-g\end{array}\right.\left\{\begin{array}{l}{v}_x=v_0\cos \alpha \\ v_y=0\\ v_z=-gt+v_0\sin \alpha \end{array}\right.\left\{\begin{array}{l}x=v_0\cos \alpha \hspace{0.17em}t\\ y=0\\ z=-{\displaystyle \frac{1}{2}}g{t}^2+v_0\sin \alpha \hspace{0.17em}t\end{array}\right.$$

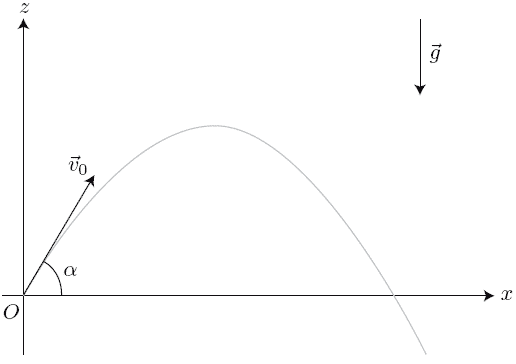
Pour trouver l'équation de la trajectoire, il suffit d'éliminer $t$ :

$$t={\displaystyle \frac{x}{v_0\cos \alpha }}z=-{\displaystyle \frac{g}{2v_0^2{\cos }^2\alpha }}\hspace{0.17em}{x}^2+\tan \alpha \hspace{0.17em}x$$

Pour trouver la portée, il faut résoudre $z=0$ :

$$\left\{\begin{array}{l}x=0\\ x={\displaystyle \frac{v_0^2\sin 2\alpha }{g}}\mathrm{maximum}\mathrm{pour}\alpha ={\displaystyle \frac{\pi }{4}}\end{array}\right.$$

Pour trouver la flêche, il faut résoudre $v_z=0$ :

$$t={\displaystyle \frac{v_0\sin \alpha }{g}}\left\{\begin{array}{l}x={\displaystyle \frac{v_0^2\sin 2\alpha }{2g}}\\ x={\displaystyle \frac{v_0^2{\sin }^2\alpha }{2g}}\end{array}\right.$$

Le point ($x_C$,0,$z_C$) est atteint par le projectile pour une vitesse $v_0$ donnée si $x_C$ et $z_C$ vérifient

$$z_C=-{\displaystyle \frac{g}{2v_0^2{\cos }^2\alpha }}\hspace{0.17em}{x}_C^2+\tan \alpha \hspace{0.17em}{x}_C$$

ou encore, si $\alpha$ est solution de l'équation

$$-{\displaystyle \frac{g{x}_C^2}{2v_0^2}}{\tan }^2\alpha +x_C\tan \alpha -{\displaystyle \frac{g{x}_C^2}{2v_0^2}}-z_C=0$$

c'est-à-dire si

$$\Delta =x_C^2-4{\displaystyle \frac{g{x}_C^2}{2v_0^2}}\left({\displaystyle \frac{g{x}_C^2}{2v_0^2}}+z_C\right)\ge 0$$

Les points accessibles du plan (Oxz) sont donc situés sous la parabole de sûreté d'équation

$$z=-{\displaystyle \frac{g}{2v_0^2}}{x}^2+{\displaystyle \frac{v_0^2}{2g}}$$

Force de frottement dans un fluide

Chute libre avec frottement proportionnel à la vitesse

Il faut rajouter la force $-k\mathbf{v}$

$$\left\{\begin{array}{l}{a}_x=-{\displaystyle \frac{k}{m}}{v}_x={\displaystyle \frac{d{v}_x}{dt}}\\ a_z=-g-{\displaystyle \frac{k}{m}}{v}_y={\displaystyle \frac{d{v}_z}{dt}}\end{array}\right.$$

On pose $\lambda ={\displaystyle \frac{k}{m}}$ et on intègre (pour $v_z$ changement de variable $u=g+\lambda v_z$)

$$\left\{\begin{array}{l}{\displaystyle \frac{d{v}_x}{v_x}}=-\lambda dt\\ {\displaystyle \frac{\lambda d{v}_z}{g+\lambda v_z}}=-\lambda dt\end{array}\right.\left\{\begin{array}{l}\ln \left({\displaystyle \frac{v_x}{v_0\cos \alpha }}\right)=-\lambda \left(t-0\right)\\ \ln \left({\displaystyle \frac{g+\lambda v_z}{g+\lambda v_0\sin \alpha }}\right)=-\lambda \left(t-0\right)\end{array}\right.$$ $$\left\{\begin{array}{l}{v}_x=\left(v_0\cos \alpha \right)\exp \left(-\lambda t\right)\\ v_z=\left({\displaystyle \frac{g}{\lambda }}+v_0\sin \alpha \right)\exp \left(-\lambda t\right)-{\displaystyle \frac{g}{\lambda }}\end{array}\right.$$

Pour $v_z$ on aurait pu résoudre une équation différentielle avec second membre

$${\displaystyle \frac{d{v}_z}{dt}}+\lambda v_z=-g$$

dont la solution est la somme solution générale de l'équation homogène sans second membre + solution particulière de l'équation avec second membre (ne marche que pour les équations différentielles linéaires)

$$v_z=\mathrm{C\; exp}\left(-\lambda t\right)-{\displaystyle \frac{g}{\lambda }}$$

On utilise les conditions initiales (sur la somme solution générale de l'équation homogène sans second membre + solution particulière de l'équation avec second membre)

$$v_z\left(t=0\right)=C-{\displaystyle \frac{g}{\lambda }}=v_0\sin \alpha$$

et on retrouve le même résultat.

On intègre une deuxième fois pour $x$ et $z$

$$\left\{\begin{array}{l}x=-{\displaystyle \frac{v_0\cos \alpha }{\lambda }}\exp \left(-\lambda t\right)+A\\ z=-{\displaystyle \frac{\left({\displaystyle \frac{g}{\lambda }}+v_0\sin \alpha \right)}{\lambda }}\exp \left(-\lambda t\right)-{\displaystyle \frac{g}{\lambda }}t+B\end{array}\right.$$

Avec les conditions initiales $x=0$ et $z=0$, on a finalement

$$\left\{\begin{array}{l}x={\displaystyle \frac{v_0\cos \alpha }{\lambda }}\left(1-\exp \left(-\lambda t\right)\right)\\ z={\displaystyle \frac{\left({\displaystyle \frac{g}{\lambda }}+v_0\sin \alpha \right)}{\lambda }}\left(1-\exp \left(-\lambda t\right)\right)-{\displaystyle \frac{g}{\lambda }}t\end{array}\right.$$

$t\to \infty$

$$\left\{\begin{array}{l}x\to {\displaystyle \frac{v_0\cos \alpha }{\lambda }}\left(\mathrm{assymptote}\right)\\ z\to -\infty \end{array}\right.et\left\{\begin{array}{l}{v}_x\to 0\\ v_z\to -{\displaystyle \frac{g}{\lambda }}=-{\displaystyle \frac{mg}{k}}=v_{\lim }\end{array}\right.$$

Pour que la vitesse limite soit atteinte, il ne faut pas que le projectile atteigne trop vite le sol.
La vitesse limite est en fait la solution particulière de l'équation

$$m{\displaystyle \frac{d\mathbf{v}}{dt}}+k\mathbf{v}=m\mathbf{g}$$

En effet lorsque la vitesse limite est atteinte ${\displaystyle \frac{d\mathbf{v}}{dt}}=0$ et

$${\mathbf{v}}_{\lim }={\displaystyle \frac{m\mathbf{g}}{k}}$$

Chute libre avec frottement proportionnel au carré de la vitesse

$$m\mathbf{a}=m\mathbf{g}-kv\mathbf{v}$$ $$\left\{\begin{array}{l}m{\displaystyle \frac{d{v}_x}{dt}}=-k\sqrt{v_x^2+v_z^2}\hspace{0.17em}{v}_x\\ m{\displaystyle \frac{d{v}_z}{dt}}=-mg-k\sqrt{v_x^2+v_z^2}\hspace{0.17em}{v}_z\end{array}\right.$$

Ce système d'équations différentielles couplées n'admet pas de solution analytique (résolution numérique) sauf dans le cas particulier du mouvement vertical :

$$m{\displaystyle \frac{d{v}_z}{dt}}=-mg-k\sqrt{v_z^2}\hspace{0.17em}{v}_z$$

Tension d'un fil

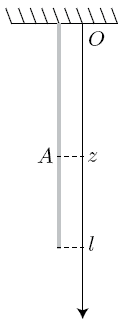
Un fil est suspendu par l'une de ses extrémités à un support.
A l'équilibre, la partie supérieure au point A exerce une force qui compense le poids de la partie inférieure de masse $m\left(l-z\right)/l$ :

$$T+mg\left(l-z\right)/l=0$$

d'où

$$T=-mg\left(l-z\right)/l$$

La tension est bien dirigée vers le haut.

Pour $z=l$, $T=0$ et pour $z=0$, $T=-mg$.

On accroche en A un objet de masse $m\text{'}$ :

$$T+mg\left(l-z\right)/l+m\text{'}g=0$$

Pour $z=l$ , $T=-m\text{'}g$.

Pour un fil idéal de masse nulle, la tension vaut $T=-m\text{'}g$ en tout point du fil.

Une poulie idéale ne modifie pas la tension (en norme) d'un fil idéal. La tension (en norme) est donc la même de chaque côté de la poulie.

Force de rappel élastique

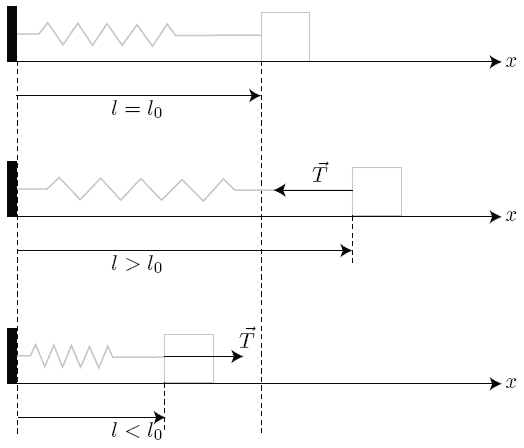
La force exercée par le ressort est proportionnel à l'allongement $X=l-l_0$ :

$$∥ T∥ =k∣ l-l_0∣$$

$k$ est la constante de raideur du ressort ($N.m^{-1}$) et $l_0$ la longueur à vide.

Si l'allongement est nul, alors $T=0$.

Si l'allongement est positif (ressort étiré) alors la tension est orientée selon $-{\mathbf{e}}_X$.

Si l'allongement est négatif (ressort comprimé) alors la tension est orientée selon ${\mathbf{e}}_X$.

Dans tous les cas, elle peut s'exprimer

$$\mathbf{T}=-kX{\mathbf{e}}_X$$

Force de liaison

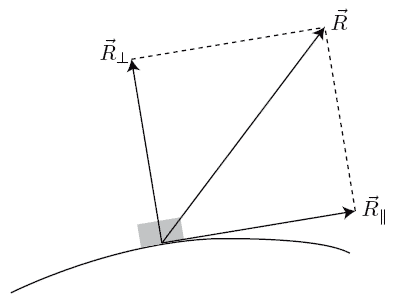
La réaction du support est la force sans laquelle le système étudié « s'enfoncerait dans le support » !

Elle est normale au support lorsqu'il n'y a pas de frottement.

Lorsqu'il y a des frottements, il existe une composante tangentielle.