Mouvement dans un champ de forces centrales conservatives

---

Les vecteurs sont notés en gras.

Forces centrales conservatives

Exemple de la force de gravitation

Soient $M_1$ de masse $m_1$ et $M_2$ de masse $m_2$

$${\mathbf{F}}_{1\to 2}=-{\mathbf{F}}_{2\to 1}=-\mathcal{G}{\displaystyle \frac{m_1{m}_2}{{\left(M_1{M}_2\right)}^2}}{\displaystyle \frac{{\mathbf{M}}_1{\mathbf{M}}_2}{M_1{M}_2}}$$

avec $\mathcal{G}=6,67.10^{-11}\hspace{0.17em}k{g}^{-1}.\hspace{0.17em}{m}^3.\hspace{0.17em}{s}^{-2}$

On supposera que $M$ de masse $m$ est attiré par un centre de force fixe $O$ de masse $m\text{'}\gg m$

$$\mathbf{F}=-\mathcal{G}{\displaystyle \frac{m\text{'}m}{r^2}}\hspace{0.17em}{\mathbf{e}}_r$$ $$\delta W=\mathbf{F}\mathrm{.d}\mathbf{OM}=-{\displaystyle \frac{A}{r^2}}\hspace{0.17em}{\mathbf{e}}_r.\left(dr\hspace{0.17em}{\mathbf{e}}_r+r\hspace{0.17em}d{\mathbf{e}}_r\right)=-A{\displaystyle \frac{dr}{r^2}}=-d{E}_p$$

avec $E_p=-{\displaystyle \frac{A}{r}}$ en prenant $E_p\left(\infty \right)=0$

Exemple de la force électrostatique

Soient $M_1$ de charge $q_1$ et $M_2$ de charge $q_2$

$${\mathbf{F}}_{1\to 2}=-{\mathbf{F}}_{2\to 1}={\displaystyle \frac{1}{4\pi {\epsilon }_0}}{\displaystyle \frac{q_1{q}_2}{{\left(M_1{M}_2\right)}^2}}{\displaystyle \frac{{\mathbf{M}}_1{\mathbf{M}}_2}{M_1{M}_2}}$$

avec ${\displaystyle \frac{1}{4\pi {\epsilon }_0}}=9.10^9\hspace{0.17em}\mathrm{S.I.}$

On supposera que $M$ de charge $q$ et de masse $m$ est attiré ou repoussé par un centre de force fixe $O$ de charge $q\text{'}$ et de masse $m\text{'}\gg m$

$$\mathbf{F}={\displaystyle \frac{1}{4\pi {\epsilon }_0}}{\displaystyle \frac{q\text{'}q}{r^2}}\hspace{0.17em}{\mathbf{e}}_r$$ $$\delta W=\mathbf{F}\mathrm{.d}\mathbf{OM}={\displaystyle \frac{B}{r^2}}\hspace{0.17em}{\mathbf{e}}_r.\left(dr\hspace{0.17em}{\mathbf{e}}_r+r\hspace{0.17em}d{\mathbf{e}}_r\right)=B{\displaystyle \frac{dr}{r^2}}=-d{E}_p$$

avec $E_p={\displaystyle \frac{B}{r}}$ en prenant $E_p\left(\infty \right)=0$

remarque : si l'on compare les forces de gravitation et électrostatique qui s'exercent par exemple entre deux électrons

$${\displaystyle \frac{F_e}{F_g}}={\left({\displaystyle \frac{e}{m}}\right)}^2\left({\displaystyle \frac{1}{4\pi {\epsilon }_0\mathcal{G}}}\right)=4,2.10^{42}$$

D'une manière générale, à l'échelle microscopique, les forces de gravitation sont négligeables devant les forces électrostatiques.

Généralisation

Force centrale si

$$\mathbf{F}=F\left(r\right)\hspace{0.17em}{\mathbf{e}}_r$$

conservative si

$$\delta W=-d{E}_p$$

Pour les forces de gravitation et électrostatique que l'on appelle interactions newtoniennes

$$F\left(r\right)={\displaystyle \frac{k}{r^2}}et{E}_p={\displaystyle \frac{k}{r}}\mathrm{avec}{E}_p\left(\infty \right)=0$$

$k=-\mathcal{G}m\text{'}m<0$ pour l'interaction gravitationnelle;

$k={\displaystyle \frac{1}{4\pi {\epsilon }_0}}\hspace{0.17em}q\text{'}q$, pour l'interaction électrostatique, négatif si $q\text{'}$ et $q$ de signe différent, positif si $q\text{'}$ et $q$ de même signe.

Lois générales de conservation

Soit M de masse $m$ et de vitesse $\mathbf{v}$ soumis à un champ de force centrale conservative $\mathbf{F}=F\left(r\right)\hspace{0.17em}{\mathbf{e}}_r$ créé par un centre de force O.

Conservation du moment cinétique

Planéité du mouvement

$${\displaystyle \frac{d{\mathbf{L}}_O}{dt}}={\mathbf{ℳ}}_O=\mathbf{OM}\wedge \mathbf{F}=r\hspace{0.17em}{\mathbf{e}}_r\wedge F\left(r\right)\hspace{0.17em}{\mathbf{e}}_r=\mathbf{0}\Rightarrow {\mathbf{L}}_O=\mathbf{cte}$$

${\mathbf{L}}_O=\mathbf{OM}\wedge m\mathbf{v}$, $\mathbf{OM}$ et $\mathbf{v}$ restent perpendiculaires à ${\mathbf{L}}_O=\mathbf{cte}$, $\mathbf{OM}$ et $\mathbf{v}$ sont donc contenus dans le plan perpendiculaire à ${\mathbf{L}}_O=\mathbf{cte}$ : le mouvement est plan.

Intégrale première du mouvement

Dans ce plan, choisissons les coordonnées polaires $\left(r,\theta \right)$

$$\mathbf{OM}=r\hspace{0.17em}{\mathbf{e}}_r\mathbf{v}=\stackrel{.}{r}\hspace{0.17em}{\mathbf{e}}_r+r\stackrel{.}{\theta }\hspace{0.17em}{\mathbf{e}}_{\theta }$$ $${\mathbf{L}}_O=\mathbf{OM}\wedge m\mathbf{v}=m{r}^2\stackrel{.}{\theta }\hspace{0.17em}{\mathbf{e}}_z$$

comme ${\mathbf{L}}_O=\mathbf{cte}$

$$\begin{array}{|c|}\hline r^2\stackrel{.}{\theta }=cte=C\\ \hline\end{array}$$

appelé intégrale première du mouvement, C constante des aires

Loi des aires

L'aire balayée par le vecteur position pendant $dt$

$$d\mathcal{𝒜}={\displaystyle \frac{1}{2}}\times r\times rd\theta ={\displaystyle \frac{1}{2}}{r}^{2}d\theta$$

La vitesse aérolaire

$${\displaystyle \frac{d\mathcal{𝒜}}{dt}}={\displaystyle \frac{1}{2}}{r}^2\stackrel{.}{\theta }={\displaystyle \frac{1}{2}}C=cte$$

Les aires balayées pendant des durées égales sont égales ce qui explique l'accélération de M lorsqu'il se rapproche du centre de force et son ralentissement lorsqu'il s'en éloigne.

Conservation de l'énergie (mécanique)

Intégrale première du mouvement

$\mathbf{F}=F\left(r\right)\hspace{0.17em}{\mathbf{e}}_r$ dérivant d'une énergie potentielle $E_p\left(r\right)$, l'énergie mécanique se conserve

$$E_m={\displaystyle \frac{1}{2}}m\left({\stackrel{.}{r}}^2+r^2{\stackrel{.}{\theta }}^2\right)+E_p\left(r\right)=cte$$

appelé intégrale première du mouvement

Energie potentielle effective

$$E_m={\displaystyle \frac{1}{2}}m{\stackrel{.}{r}}^2+{\displaystyle \frac{1}{2}}m{r}^2{\stackrel{.}{\theta }}^2+E_p\left(r\right)$$

${\displaystyle \frac{1}{2}}m{r}^2{\stackrel{.}{\theta }}^2={\displaystyle \frac{m}{2r^2}}{\left(r^2\stackrel{.}{\theta }\right)}^2={\displaystyle \frac{m}{2r^2}}{C}^2$

$$E_m={\displaystyle \frac{1}{2}}m{\stackrel{.}{r}}^2+{\displaystyle \frac{m{C}^2}{2r^2}}+E_p\left(r\right)$$

L'énergie mécanique ne dépend plus que de $\stackrel{.}{r}$ et $r$ :

le terme ${\displaystyle \frac{1}{2}}m{\stackrel{.}{r}}^2$ est appelé énergie cinétique radiale

le terme ${\displaystyle \frac{m{C}^2}{2r^2}}+E_p\left(r\right)=E_{p\mathrm{,\; eff}}$ est appelé énergie potentielle effective

$$\begin{array}{|c|}\hline E_m={\displaystyle \frac{1}{2}}m{\stackrel{.}{r}}^2+{E_p}_{eff}\left(r\right)=cte\\ \hline\end{array}$$

Etats de diffusion, états liés

Le terme cinétique ${\displaystyle \frac{1}{2}}m{\stackrel{.}{r}}^2$ étant positif, $E_m=cte$ est la plus grande valeur que puisse prendre ${E_p}_{eff}\left(r\right)$; les valeurs de $r$ pour lesquelles $E_{p\mathrm{,\; eff}}>E_m$ sont donc inaccessibles.

Si $r>r_{\min }$, on parle d'état de diffusion

Si $r_{\min }\le r\le r_{\max }$, on parle d'état lié

Mouvement dans un champ de force centrales newtonien

Le mouvement vérifie les propriétés générales du mouvement dans un champ de forces centrales conservatives (planéité du mouvement, loi des aires, énergie potentielle effective) avec $F\left(r\right)={\displaystyle \frac{k}{r^2}}$ et $E_p={\displaystyle \frac{k}{r}}$

Equation générale de la trajectoire

On peut alors montrer que la trajectoire du point M, repéré par ses coordonnées polaires a pour équation (en choisissant Ox axe de symétrie de la trajectoire)

$$r\left(\theta \right)={\displaystyle \frac{p}{1+\mathrm{e\; cos}\theta }}$$

On reconnaît l'équation d'une conique

si $e>1$, M décrit une hyperbole

si $e=1$, M décrit une parabole

si $0<e<1$, M décrit une ellipse

si $e=0$, M décrit un cercle

Interaction répulsive

$$k>0$$

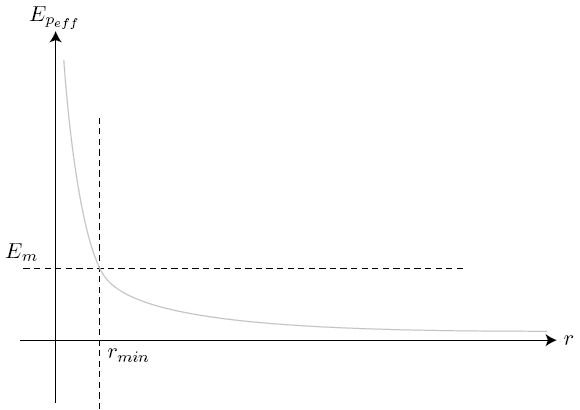
$r>r_{\min }$, état de diffusion, M ne peut pas s'approcher du centre de force à une distance inférieure à $r_{\min }$, cette position extrême s'appelle le péricentre.

La trajectoire correspondante correspond à une branche d'hyperbole.

Interaction attractive

$$k<0$$

Etat de diffusion

$$E_m>0$$

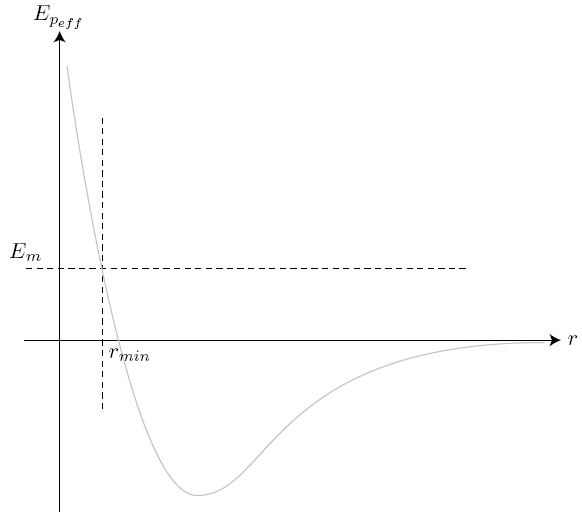
$r>r_{\min }$, on observe encore un état de diffusion.

La trajectoire est encore une branche d'hyperbole.

Le cas particulier $E_m=0$ correspond à une trajectoire parabolique.

Etat lié

$${{E_p}_{eff}}_{\min }<E_m<0$$

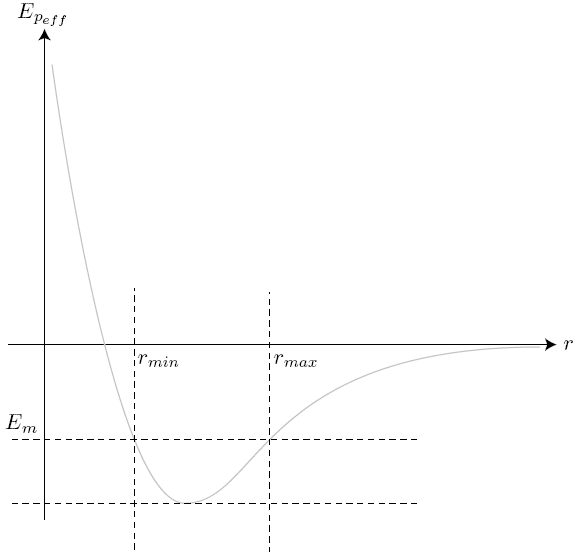
$r_{\min }\le r\le r_{\max }$, état lié, la position de M correspondant à $r_{\min }$ est appelée péricentre, celle correspondant à $r_{\max }$ apocentre.

La trajectoire est elliptique.

Le cas particulier $r_{\min }=r_{\max }=R$ correspond à une trajectoire circulaire.

Mouvements des planètes - Lois de Képler

Lois de Képler

Ces lois historiques concernent les mouvements des planètes autour du Soleil, elles se généralisent à tous les mouvements à force gravitationnelle centrale.

Première loi : les planètes autour du Soleil décrivent des ellipses dont l'un des foyers est occupé par le Soleil.

Deuxième loi : le mouvement d'une planète obéit à la loi des aires.

Pendant des durées égales $\Delta t$, le rayon vecteur $\mathbf{OM}$ balaye des aires égales $S={\displaystyle \frac{C}{2}}\Delta t$ où $C$ est la constante des aires liée à la planète considérée.

Troisième loi : $${\displaystyle \frac{T^2}{a^3}}={\displaystyle \frac{4{\pi }^2}{\mathcal{G}m\text{'}}}$$

où $T$ est la période de révolution elliptique de la planète autour du Soleil, $a$ le demi grand-axe de la trajectoire elliptique et $m\text{'}=m_S$ la masse du Soleil; la masse de la planète n'intervient pas.

Vitesses cosmiques

La vitesse circulaire est la vitesse à communiquer initialement à un corps pour qu'il décrive une orbite circulaire de rayon $a$ autour d'un gros astre de masse $m\text{'}$ :

$$E_m=-{\displaystyle \frac{∣ k∣ }{2a}}$$ $${\displaystyle \frac{1}{2}}m{v}_c^2-{\displaystyle \frac{∣ k∣ }{a}}=-{\displaystyle \frac{∣ k∣ }{2a}}\Rightarrow v_c=\sqrt{{\displaystyle \frac{\mathcal{G}m\text{'}}{a}}}$$

La vitesse de libération est la vitesse à communiquer initialement à un corps pour qu'il échappe à l'attraction d'un gros astre de masse $m\text{'}$ :

$${\displaystyle \frac{1}{2}}m{v}_l^2-{\displaystyle \frac{∣ k∣ }{r_0}}=0\Rightarrow v_l=\sqrt{{\displaystyle \frac{2\mathcal{G}m\text{'}}{r_0}}}$$