Introduction à la mécanique classique - Rappels et domaine de validité

Les vecteurs sont notés en gras.

Première loi de Newton ou principe d'inertie

Dans un référentiel galiléen, un point matériel isolé à un mouvement rectiligne uniforme.

Qu'est-ce qu'un mouvement rectiligne uniforme ? Un mouvement rectiligne uniforme est un mouvement pour lequel $v = cte$

direction constante $\to$ rectiligne

norme constante $\to$ uniforme

immobilité cas particulier $v = 0$

Qu'est-ce qu'un point matériel isolé ? C'est un point affecté d'une masse qui n'est soumis à aucune force.

C'est une situation idéale car un objet est toujours soumis à des forces, ces forces pouvant éventuellement être négligeables ou se compenser; on parle alors d'objet pseudo-isolé.

Qu'est-ce qu'un référentiel ?

Un référentiel va nous permettre de répondre aux questions où ? et quand ? En effet, pour décrire un mouvement, il faut pouvoir préciser à la fois où se trouve le point et à quel instant il s'y trouve. Pour préciser où se trouve le point, on utilisera un repère et pour préciser à quel instant il s'y trouve, on utilisera une horloge :

référentiel = repère + horloge

Qu'est-ce qu'un référentiel galiléen ? Un référentiel galiléen est un référentiel dans lequel un point matériel isolé à un mouvement rectiligne uniforme.

Seule l'expérience pourra nous dire si un référentiel est galiléen ou pas.

Deuxième loi de Newton ou principe fondamental de la dynamique

Enoncé

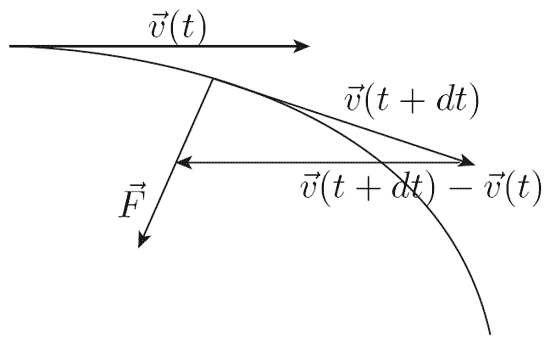
Le mouvement est donc modifié par les forces. Un mouvement est modifié si la direction du vecteur vitesse et/ou sa norme varie $v \neq cte$ ou encore $a \neq 0$ puisque

a = \frac{d v}{d t}

où $d v = v (t + d t) - v (t)$ est la variation infinitésimale du vecteur vitesse entre les instants $t$ et $t + d t$ .

La deuxième loi de Newton est la relation entre la modification du mouvement (accélération) et sa cause (force) :

Dans un référentiel galiléen $m a = F$

où $F$ est la résultante des forces appliquées au point matériel de masse $m$ dont l'accélération est $a$ .

Le principe d'inertie est le cas particulier du principe fondamental

F = 0 \Rightarrow a = 0 \Rightarrow v = cte

La masse (inertielle) est donc un coefficient de proportionnalité; pour $F$ donnée, la modification du mouvement est d'autant plus grande que $m$ est petit (il est plus facile de modifier le mouvement d'un vélo que celui d'un camion !).

Exploitation

Solution analytique

Etudions le mouvement d'un projectile de masse $m$ lancée avec une vitesse initiale $v_{0}$ dans le champ de pesanteur terrestre (on négligera les frottements)

Système étudié : projectile assimilable à un point matériel de masse $m$

Référentiel : repère Oxyz (classe) supposé galiléen + horloge (on l'oublie souvent car le temps est universel en mécanique classique).

Bilan des forces : poids

Loi fondamentale : $m a = m g$

Projection :

∣\begin{array}{l} a_{x} \\ a_{y} \\ a_{z} \end{array} = ∣\begin{array}{l} 0 \\ - g \\ 0 \end{array}

ce qui donne après intégration :

y = - \frac{g}{2 v_{0_{x}}^{2}} x^{2} + \frac{v_{0_{y}}}{v_{0_{x}}} x

C'est une solution analytique, on a une fonction mathématique qui nous donne tous les points de la trajectoire.
Lorsqu'il n'existe pas de solution analytique on a recours à des méthodes numériques où l'on calcule chaque point de la trajectoire.

Solution numérique

cf TP

Peut-on résoudre n'importe quel problème ?

Les problèmes qui ont une solution analytique sont rares et correspondent souvent à des situations idéales.
La résolution numérique est toujours possible encore faut-il que la deuxième loi de Newton puisse s'appliquer au problème.
Plusieurs fois dans l'histoire, on a cru trouver des situations remettant en cause cette loi et plusieurs fois le problème fut résolu.
Exemple : en fait le mouvement d'une planète autour du Soleil n'est pas vraiment une ellipse mais on peut trouver les corrections en tenant compte de l'attraction des autres planètes. A l'époque, on a fait ces calculs et çà marchait sauf pour Uranus. Le Verrier (1811-1877) eu l'idée d'attribuer la différence observée à une planète invisible. On calcula la position de cette planète invisible, on pointa un télescope dans la direction calculée, la planète était là (Neptune)! Ce fut un grand succès pour la deuxième loi.
Pendant longtemps on cru que seuls une analyse incomplète ou des calculs trop lourds pouvaient mettre en défaut la deuxième loi.
Or même en tenant de toutes les forces et avec une capacité de calcul illimitée, il y a des domaines où la deuxième loi ne s'applique pas :

domaine microscopique $\to$ mécanique quantique
domaine $v ≃ c$ $\to$ relativité

Troisième loi de Newton ou principe de l'action et de la réaction

Enoncé

Les forces d'interaction réciproque qui s'exercent entre deux points matériels sont opposées et ont pour support la droite joignant ces points.

Une conséquence

Le principe d'inertie ou la deuxième loi de Newton s'applique à un point matériel. Pourquoi peut-on l'appliquer à une planète par exemple ?

On "découpe" la planète en morceaux assez petits pour pouvoir les considérer comme des points matériels de masse $m_{i}$ tels que $\sum_{i} m_{i} = m$ masse de la planète. On peut alors appliquer la deuxième loi à chaque point :

$m_{i} a_{i} =$ forces exercées par les autres points (forces intérieures) + les autres forces (forces extérieures)

m_{i} a_{i} = \sum_{j \neq i} f_{j \to i} + f_{e x t \to i}

\sum_{i} m_{i} a_{i} = \sum_{i} \sum_{j \neq i} f_{j \to i} + \sum_{i} f_{e x t \to i}

= 0 + F_{e x t \to planete}

Vérifier pour $i = 3$ par exemple

\sum_{i} m_{i} a_{i} = \sum_{i} m_{i} \frac{d^{2} {OM}_{i}}{d t^{2}} = \frac{d^{2}}{d t^{2}} \sum_{i} m_{i} {OM}_{i} = \frac{d^{2}}{d t^{2}} m OG

= m a (G)

Quand on assimile un système à un point matériel, on étudie en fait le mouvement d'un point particulier appelé barycentre ou centre d'inertie ou centre de gravité et on ne tient compte que des forces extérieures au système.

accueil > matières > mécanique > introduction à la mécanique classique