Dynamique du point matériel en référentiel galiléen (suite)

---

Les vecteurs sont notés en gras.

Moment cinétique

Soit, dans un référentiel $ℛ$, un point matériel M de masse $m$, de vecteur vitesse $\mathbf{v}$ et $\mathbf{F}$ la résultante des forces appliquées en M.
Soit O un autre point de $ℛ$.

Définitions

La grandeur

$$\begin{array}{|c|}\hline {\mathbf{L}}_O=\mathbf{OM}\wedge m\mathbf{v}\\ \hline\end{array}$$

est appelée moment cinétique en O du point M.

La grandeur

$$\begin{array}{|c|}\hline {\mathbf{ℳ}}_O=\mathbf{OM}\wedge \mathbf{F}\\ \hline\end{array}$$

est appelée moment en O de la résultante des forces $\mathbf{F}$ appliquée au point M.

Théorème du moment cinétique en un point fixe

Soit O un point fixe d'un référentiel galiléen $ℛ$ :

$${\displaystyle \frac{d{\mathbf{L}}_O}{dt}}={\displaystyle \frac{d\mathbf{OM}}{dt}}\wedge m\mathbf{v}+\mathbf{OM}\wedge m{\displaystyle \frac{d\mathbf{v}}{dt}}=\mathbf{0}+\mathbf{OM}\wedge m\mathbf{a}$$

la deuxième loi de Newton donne :

$${\displaystyle \frac{d{\mathbf{L}}_O}{dt}}=\mathbf{OM}\wedge \mathbf{F}$$

d'où le théorème du moment cinétique :

$$\begin{array}{|c|}\hline {\displaystyle \frac{d{\mathbf{L}}_O}{dt}}={\mathbf{ℳ}}_O\\ \hline\end{array}$$

Dans un référentiel galiléen, la dérivée du moment cinétique en un point fixe O par rapport au temps est égale au moment en O de la résultante des forces qui s'appliquent au point M.

Théorème du moment cinétique par rapport à un axe fixe

Soit $\Delta$ un axe passant par O, de vecteur directeur $\mathbf{u}$.

Moment d'une force par rapport à un axe

La grandeur

$$\begin{array}{|c|}\hline {ℳ}_{\Delta }={\mathbf{ℳ}}_O.\mathbf{u}\\ \hline\end{array}$$

est appelée moment par rapport à $\Delta$ de la résultante des forces $\mathbf{F}$ appliquée au point M.

Si $\mathbf{F}$ est parallèle à $\Delta$ alors ${ℳ}_{\Delta }=\left(\mathbf{OM}\wedge \mathbf{F}\right).\mathbf{u}=0$

Si $\mathbf{F}$ est perpendiculaire à $\Delta$ alors

$${ℳ}_{\Delta }=\left(\left(\mathbf{O}{\mathbf{H}}_1+{\mathbf{H}}_1{\mathbf{H}}_2+{\mathbf{H}}_2\mathbf{M}\right)\wedge \mathbf{F}\right).\mathbf{u}=\left({\mathbf{H}}_1{\mathbf{H}}_2\wedge \mathbf{F}\right).\mathbf{u}=\pm H_1{H}_2\mathrm{.F}=\pm Fd$$

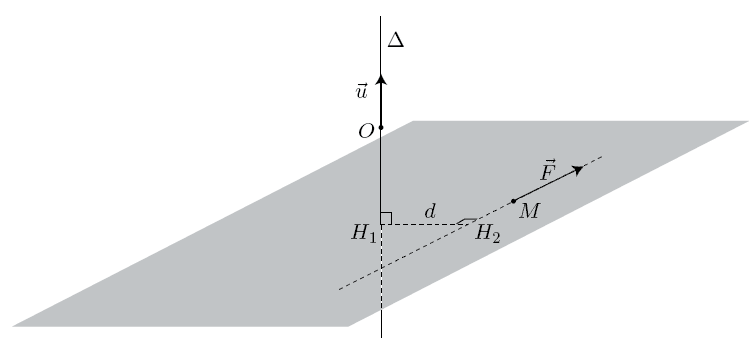
Moment cinétique par rapport à un axe

La grandeur

$$\begin{array}{|c|}\hline L_{\Delta }={\mathbf{L}}_O.\mathbf{u}\\ \hline\end{array}$$

est appelée moment cinétique par rapport à $\Delta$ du point M.

Théorème du moment cinétique par rapport à un axe

Soit $\Delta$ un axe fixe passant par O, de vecteur directeur $\mathbf{u}$. En projetant le théorème du moment cinétique suivant $\mathbf{u}$ :

$$\begin{array}{|c|}\hline {\displaystyle \frac{d{L}_{\Delta }}{dt}}={ℳ}_{\Delta }\\ \hline\end{array}$$

Dans un référentiel galiléen, la dérivée du moment cinétique par rapport à $\Delta$ par rapport au temps est égale au moment par rapport à $\Delta$ de la résultante des forces qui s'appliquent au point M.