énergie potentielle - Oscillateur harmonique - Régime libre

---

Les vecteurs sont notés en gras.

Oscillateur harmonique

On appelle oscillateur harmonique tout système à un degré de liberté dont l'évolution au cours du temps (en l'absence d'amortissement et d'excitation) est régi par l'équation différentielle suivante : $${\displaystyle \frac{d^{2}x}{d{t}^2}}+{\omega }_0^2\hspace{0.17em}x=0$$ quelle que soit la nature physique de la variable $x$.

L'oscillateur harmonique évolue dans un puit de potentiel de type parabolique :

soit

$$E_p\left(x\right)=E_p\left(0\right)+{\displaystyle \frac{1}{2}}k{x}^2$$

soit

$$E_p\left(x\right)\simeq E_p\left(0\right)+{\displaystyle \frac{1}{2}}k{x}^2$$

au voisinage d'une position d'équilibre stable (voir cours précédent).

L'oscillateur harmonique est soumis à une force de rappel proportionnelle à $x$ :

$$F=-{\displaystyle \frac{d{E}_p}{dx}}=-kx$$

Oscillations libres

Pulsation propre - Isochronisme des oscillations

$$x\left(t\right)=x_m\cos \left({\omega }_{0}t+\varphi \right)$$ $$\stackrel{.}{x}\left(t\right)=-x_m{\omega }_0\sin \left({\omega }_{0}t+\varphi \right)=v\left(t\right)$$

$x_m$ et $\varphi$ sont déterminés par les conditions initiales.
Si $x\left(0\right)=0$ et $v\left(0\right)=v_0$ alors

$$\left\{\begin{array}{l}{x}_m=\sqrt{x_0^2+{\left({\displaystyle \frac{v_0}{{\omega }_0}}\right)}^2}\\ \tan \varphi =-{\displaystyle \frac{v_0}{{\omega }_0{x}_0}}\end{array}\right.$$

La période $T={\displaystyle \frac{2\pi }{{\omega }_0}}$ est indépendante des conditions initiales; c'est une propriété importante de l'oscillateur harmonique appelée isochronisme des oscillations.

Etude énergétique

$$E_m=E_c+E_p={\displaystyle \frac{1}{2}}m{x}_m^2{\omega }_0^2{\sin }^2\left({\omega }_{0}t+\varphi \right)+{\displaystyle \frac{1}{2}}k{x}_m^2{\cos }^2\left({\omega }_{0}t+\varphi \right)={\displaystyle \frac{1}{2}}k{x}_m^2$$

Calculons la valeur moyenne de $E_p$

$$\langle E_p\rangle ={\displaystyle \frac{1}{T}}\underset{0}{\overset{T}{\int }}{E}_p\left(t\right)dt={\displaystyle \frac{k{x}_m^2}{2}}\langle {\cos }^2\left({\omega }_{0}t+\varphi \right)\rangle ={\displaystyle \frac{k{x}_m^2}{4}}$$

de même

$$\langle E_c\rangle ={\displaystyle \frac{k{x}_m^2}{4}}$$

Pendant le mouvement, il y a équipartition, en moyenne, des formes cinétique et potentielle de l'énergie. $$\langle E_p\rangle =\langle E_c\rangle ={\displaystyle \frac{E_m}{2}}$$

Oscillations libres amorties

Temps de relaxation - Facteur de qualité

Avec amortissement, l'équation différentielle devient

$$m\stackrel{..}{x}=-kx-h\stackrel{.}{x}$$

que l'on met sous la forme

$$\stackrel{..}{x}+2\alpha \stackrel{.}{x}+{\omega }_0^{2}x=0$$

avec $2\alpha ={\displaystyle \frac{h}{m}}$ et ${\omega }_0^2={\displaystyle \frac{k}{m}}$, ou encore

$$\stackrel{..}{x}+{\displaystyle \frac{\stackrel{.}{x}}{\tau }}+{\omega }_0^{2}x=0$$

où $\tau$ est une constante ayant la dimension d'un temps qui est appelée temps de relaxation de l'oscillateur, ${\omega }_0$ étant sa pulsation propre.

Pour décrire l'oscillateur amorti, on peut préférer au couple (${\omega }_0$, $\tau$) le couple ( ${\omega }_0$,$Q$), $Q$ étant un paramètre sans dimension appelé facteur de qualité défini par

$$Q={\omega }_0\tau =2\pi {\displaystyle \frac{\tau }{T_0}}={\displaystyle \frac{{\omega }_0}{2\alpha }}={\displaystyle \frac{m{\omega }_0}{h}}$$

Une solution en $\exp \left(rt\right)$ existe si

$$r^2+2\alpha r+{\omega }_0^2=0$$

Suivant le signe du discriminant réduit, plusieurs régimes sont possibles

$$\Delta \text{'}={\alpha }^2-{\omega }_0^2$$

Régime pseudo-périodique

Si les frottements sont faibles alors $\alpha <{\omega }_0$, $Q>{\displaystyle \frac{1}{2}}$ et $\Delta \text{'}<0$

$$x\left(t\right)={\mathrm{e}}^{-\alpha t}\left(\mathrm{A\; cos}\Omega t+\mathrm{B\; sin}\Omega t\right)$$

en introduisant la pseudo-pulsation $\Omega$ telle que ${\Omega }^2={\omega }_0^2-{\alpha }^2$ ( $\Delta \text{'}=-{\Omega }^2={\left(i\Omega \right)}^2$ et $r=-\alpha \pm i\Omega$ )

$$\stackrel{.}{x}=-\alpha {\mathrm{e}}^{-\alpha t}\left(\mathrm{A\; cos}\Omega t+\mathrm{B\; sin}\Omega t\right)+{\mathrm{e}}^{-\alpha t}\Omega \left(-\mathrm{A\; sin}\Omega t+\mathrm{B\; cos}\Omega t\right)$$ $$\left\{\begin{array}{l}x\left(0\right)=A=x_0\\ \stackrel{.}{x}\left(0\right)=-\alpha A+\Omega B=v_0\end{array}\right.$$ $$\begin{array}{|c|}\hline x\left(t\right)={\mathrm{e}}^{-\alpha t}\left(x_0\cos \Omega t+{\displaystyle \frac{v_0+\alpha x_0}{\Omega }}\sin \Omega t\right)\\ \hline\end{array}$$

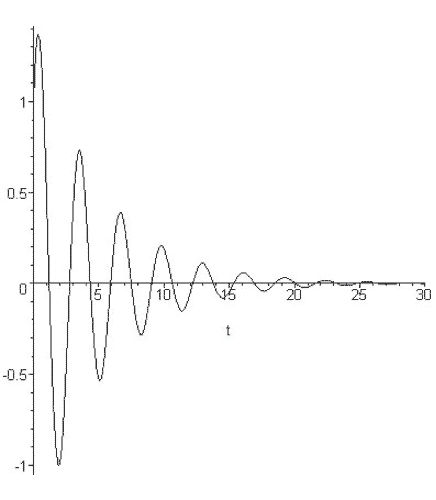
Une telle évolution de retour vers un état permanent est qualifiée de relaxation; ce retour se fait au bout de quelques $\tau$.

$T={\displaystyle \frac{2\pi }{\Omega }}={\displaystyle \frac{T_0}{\sqrt{1-{\left({\displaystyle \frac{\alpha }{{\omega }_0}}\right)}^2}}}={\displaystyle \frac{T_0}{\sqrt{1-{\displaystyle \frac{1}{4Q^2}}}}}$ est la pseudo-période.

La détermination expérimentale de $\delta =\ln \left({\displaystyle \frac{x\left(t\right)}{x\left(t+T\right)}}\right)$ appelé décrément logarithmique permet de calculer le facteur de qualité

$$\delta =\alpha T={\displaystyle \frac{{\omega }_{0}T}{2Q}}={\displaystyle \frac{\pi }{\sqrt{Q^2-{\displaystyle \frac{1}{4}}}}}$$

Régime apériodique

Si les frottements sont importants alors $\alpha >{\omega }_0$, $Q<{\displaystyle \frac{1}{2}}$ et $\Delta \text{'}>0$

$$x\left(t\right)={\mathrm{e}}^{-\alpha t}\left(\mathrm{A\; cosh}\Omega \text{'}t+\mathrm{B\; sin}\Omega \text{'}t\right)$$

avec $\Omega {\text{'}}^2={\alpha }^2-{\omega }_0^2$ ($r=-\alpha \pm \Omega \text{'}$)

$$\stackrel{.}{x}=-\alpha {\mathrm{e}}^{-\alpha t}\left(\mathrm{A\; cosh}\Omega \text{'}t+\mathrm{B\; sin}\Omega \text{'}t\right)+{\mathrm{e}}^{-\alpha t}\Omega \text{'}\left(\mathrm{A\; sin}\Omega \text{'}t+\mathrm{B\; cosh}\Omega \text{'}t\right)$$ $$\left\{\begin{array}{l}x\left(0\right)=A=x_0\\ \stackrel{.}{x}\left(0\right)=-\alpha A+\Omega \text{'}B=v_0\end{array}\right.$$ $$\begin{array}{|c|}\hline x\left(t\right)={\mathrm{e}}^{-\alpha t}\left(x_0\cosh \Omega \text{'}t+{\displaystyle \frac{v_0+\alpha x_0}{\Omega \text{'}}}\sin \Omega \text{'}t\right)\\ \hline\end{array}$$

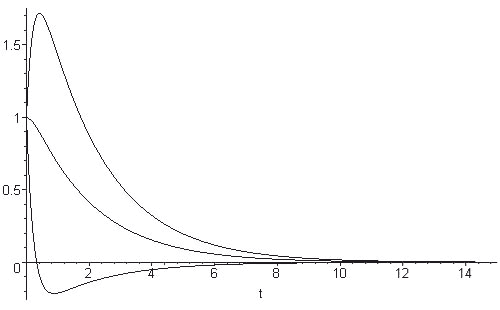
Régime critique

Si $\alpha ={\omega }_0$, $Q={\displaystyle \frac{1}{2}}$ et $\Delta \text{'}=0$

$$x\left(t\right)={\mathrm{e}}^{-\alpha t}\left(At+B\right)$$

($r=-\alpha$)

$$\stackrel{.}{x}=-\alpha {\mathrm{e}}^{-\alpha t}\left(At+B\right)+{\mathrm{e}}^{-\alpha t}A$$ $$\left\{\begin{array}{l}x\left(0\right)=B=x_0\\ \stackrel{.}{x}\left(0\right)=-\alpha B+A=v_0\end{array}\right.$$ $$\begin{array}{|c|}\hline x\left(t\right)={\mathrm{e}}^{-\alpha t}\left(\left(v_0+\alpha x_0\right)t+x_0\right)\\ \hline\end{array}$$

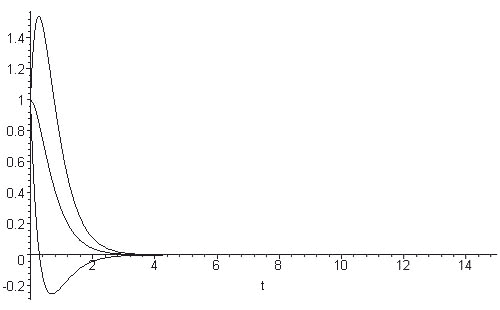
Le régime critique n'est jamais réalisé physiquement exactement.

Etude énergétique

$${\displaystyle \frac{d{E}_m}{dt}}={\mathcal{P}}^{nc}=-h{v}^2<0$$