oscillateur harmonique - régime sinusoïdal forcé

---

Les vecteurs sont notés en gras.

C'est la suite du cours « Oscillateur harmonique - Régime libre ». On se limitera à une excitation sinusoïdale.

Oscillateur harmonique amorti par frottement visqueux et soumis à une excitation sinusoïdale

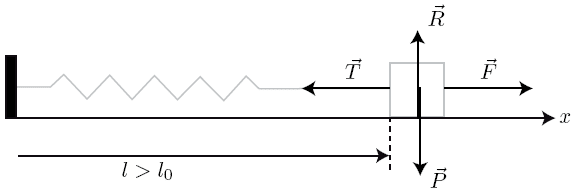
Nous retrouvons les forces du régime libre (force de rappel, amortissement qui n'est pas représentée sur la figure car elle dépend de la vitesse) qui constituent la partie homogène de l'équation différentielle plus la force excitatrice qui constitue le second membre :

$$m\stackrel{..}{x}=-kx-h\stackrel{.}{x}+F_0\cos \omega t$$ $$\stackrel{..}{x}+2\alpha \stackrel{.}{x}+{\omega }_0^{2}x={\displaystyle \frac{F_0}{m}}\cos \omega t$$

avec $2\alpha ={\displaystyle \frac{h}{m}}$ et ${\omega }_0^2={\displaystyle \frac{k}{m}}$

Régime transitoire

La solution est la somme :

$$x=x^{\left(h\right)}+x^{\left(p\right)}$$

$x^{\left(h\right)}$, solution homogène, est solution de

$$\stackrel{..}{x}+2\alpha \stackrel{.}{x}+{\omega }_0^{2}x=0$$

La solution de cette équation différentielle tend vers 0 au bout de quelques $\tau ={\displaystyle \frac{1}{2\alpha }}$ (voir cours « Oscillateur harmonique - Régime libre »).

$x^{\left(p\right)}$, solution particulière, est de la forme

$$x^{\left(p\right)}=X_m\cos \left(\omega t+\varphi \right)$$

La solution particulière oscille avec la même pulsation que l'excitation.

On parle de régime transitoire tant que $x^{\left(h\right)}$ n'est pas négligeable.

Régime sinusoïdal forcé - Utilisation des complexes

On parle de régime sinusoïdal forcé lorsque $x^{\left(h\right)}$ devient négligeable

$$x=x^{\left(h\right)}+x^{\left(p\right)}\simeq x^{\left(p\right)}$$

On travaille alors avec les complexes

$$\underset{¯}{x}=X_m\exp j\left(\omega t+\varphi \right)={\underset{¯}{X}}_m\exp j\omega t$$

avec ${\underset{¯}{X}}_m=X_m\exp j\varphi$

$\underset{¯}{x}$ est solution de

$$\stackrel{..}{\underset{¯}{x}}+2\alpha \stackrel{.}{\underset{¯}{x}}+{\omega }_0^2\underset{¯}{x}={\displaystyle \frac{F_0}{m}}\exp j\omega t$$

qui devient

$$\left(-{\omega }^2+2\alpha j\omega +{\omega }_0^2\right){\underset{¯}{X}}_m={\displaystyle \frac{F_0}{m}}$$ $${\underset{¯}{X}}_m={\displaystyle \frac{{\displaystyle \frac{F_0}{m}}}{{\omega }_0^2-{\omega }^2+\mathrm{j2}\alpha \omega }}$$

Résonance en élongation

L'amplitude $X_m$ est égale au module de ${\underset{¯}{X}}_m$

$$X_m=∣ {\underset{¯}{X}}_m∣ ={\displaystyle \frac{{\displaystyle \frac{F_0}{m}}}{\sqrt{{\left({\omega }_0^2-{\omega }^2\right)}^2+4{\alpha }^2{\omega }^2}}}$$

que l'on peut aussi écrire en introduisant le facteur de qualité $Q$ et le rapport ${\displaystyle \frac{\omega }{{\omega }_0}}=x$

$$X_m={\displaystyle \frac{{\displaystyle \frac{F_0}{k}}}{\sqrt{{\left(1-x^2\right)}^2+{\displaystyle \frac{x^2}{Q^2}}}}}$$

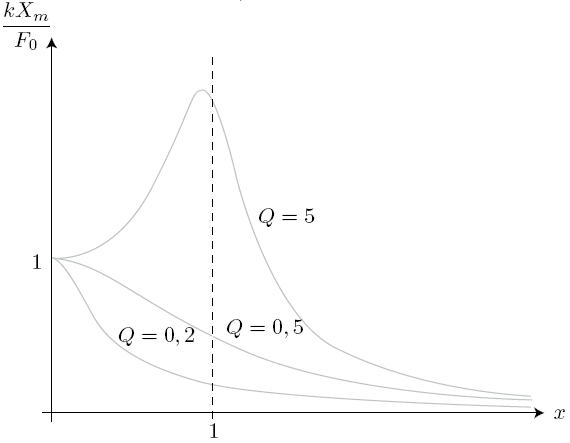
Il y a résonance en élongation seulement si $Q>{\displaystyle \frac{1}{\sqrt{2}}}$ (voir le cours d'électrocinétique «Régime sinusoïdal forcé»).

Le déphasage $\varphi$ est égale à l'argument de ${\underset{¯}{X}}_m$

$$\varphi =\arg {\underset{¯}{X}}_m=-\arctan {\displaystyle \frac{2\alpha \omega }{{\omega }_0^2-{\omega }^2}}=-\arctan {\displaystyle \frac{x}{Q\left(1-x^2\right)}}$$

Résonance en vitesse

$v={\displaystyle \frac{dx}{dt}}$

$$\underset{¯}{v}={\displaystyle \frac{d\underset{¯}{x}}{dt}}=j\omega \underset{¯}{x}=j\omega {\underset{¯}{X}}_m\exp j\omega t={\underset{¯}{V}}_m\exp j\omega t$$ $${\underset{¯}{V}}_m=j\omega {\underset{¯}{X}}_m=j\omega {\displaystyle \frac{{\displaystyle \frac{F_0}{m}}}{{\omega }_0^2-{\omega }^2+\mathrm{j2}\alpha \omega }}$$

L'amplitude $V_m$ est égale au module de ${\underset{¯}{V}}_m$

$$V_m=∣ {\underset{¯}{V}}_m∣ =\omega {\displaystyle \frac{{\displaystyle \frac{F_0}{m}}}{\sqrt{{\left({\omega }_0^2-{\omega }^2\right)}^2+4{\alpha }^2{\omega }^2}}}$$

que l'on peut aussi écrire en introduisant le facteur de qualité $Q$ et le rapport ${\displaystyle \frac{\omega }{{\omega }_0}}=x$

$$V_m={\displaystyle \frac{{\displaystyle \frac{F_0}{h}}}{\sqrt{1+Q^2{\left(x-{\displaystyle \frac{1}{x}}\right)}^2}}}$$

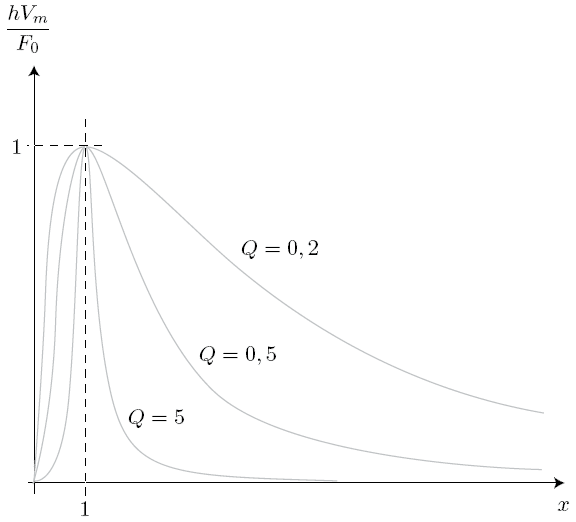
Il y a toujours résonance en vitesse.

Le déphasage ${\varphi }_v$ est égale à l'argument de ${\underset{¯}{V}}_m$

$${\varphi }_v=\arg {\underset{¯}{V}}_m={\displaystyle \frac{\pi }{2}}-\arctan {\displaystyle \frac{2\alpha \omega }{{\omega }_0^2-{\omega }^2}}={\displaystyle \frac{\pi }{2}}+\varphi$$