Repérage d'un point - Vitesse et accélération (2)

---

Les vecteurs sont notés en gras.

Coordonnées curvilignes - Base de Frénet

Repérage d'un point - Abscisse curviligne

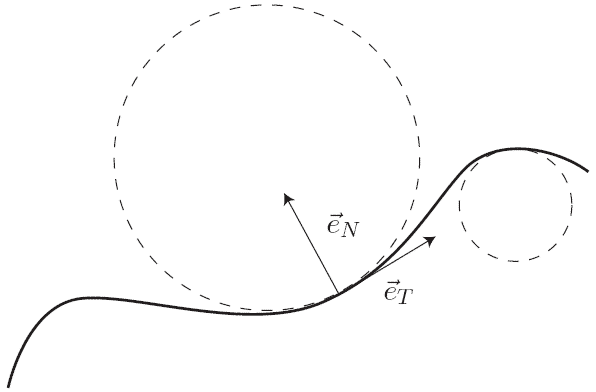
On repère le point sur sa trajectoire (courbe orientée) par son abscisse curviligne :

$$\begin{array}{|c|}\hline s=SM\\ \hline\end{array}$$

${\mathbf{e}}_T$ et ${\mathbf{e}}_N$ forment la base de Frénet.

${\mathbf{e}}_T$ est le vecteur unitaire tangent à la trajectoire orienté selon le sens positif; ${\mathbf{e}}_N$ s'obtient en tournant de $\pi /2$ vers l'intérieur de la concavité.

Vecteur vitesse et vecteur accélération

$$\begin{array}{|c|}\hline \mathbf{v}=v\hspace{0.17em}{\mathbf{e}}_T\\ \hline\end{array}\mathrm{avec}v={\displaystyle \frac{ds}{dt}}$$ $$\begin{array}{|c|}\hline \mathbf{a}={\displaystyle \frac{dv}{dt}}{\mathbf{e}}_T+{\displaystyle \frac{v^2}{R_c}}{\mathbf{e}}_N\\ \hline\end{array}$$

$a_T={\displaystyle \frac{dv}{dt}}$ est la composante tangentielle de l'accélération.

$a_N={\displaystyle \frac{v^2}{R_c}}$ est la composante normale de l'accélération.

Pourquoi $\mathbf{a}\ne \stackrel{.}{v}\hspace{0.17em}{\mathbf{e}}_T$ ?

Quand on dérive (par rapport au temps), il faut toujours faire le point sur ce qui dépend du temps.

$v\left(t\right)$ mais aussi ${\mathbf{e}}_T\left(t\right)$ !

Donc $\mathbf{a}={\displaystyle \frac{dv}{dt}}{\mathbf{e}}_T+v{\displaystyle \frac{d{\mathbf{e}}_T}{dt}}$; en identifiant ${\displaystyle \frac{v^2}{R_c}}{\mathbf{e}}_N=v{\displaystyle \frac{d{\mathbf{e}}_T}{dt}}$ ou encore

$${\mathbf{e}}_N={\displaystyle \frac{R_c}{v}}{\displaystyle \frac{d{\mathbf{e}}_T}{dt}}$$

Coordonnées polaires et cylindriques

Repérage d'un point - Vecteur position

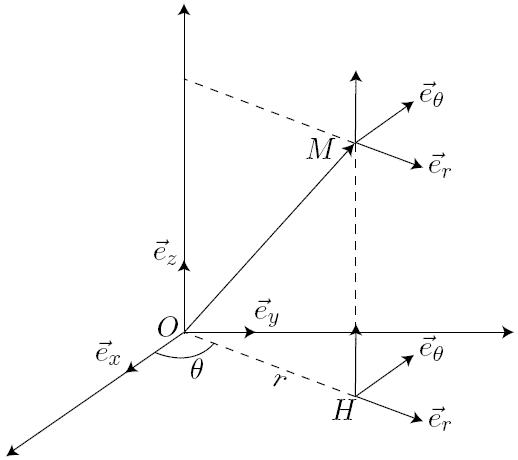
De la même manière que $x={\overline{OH}}_x$, $y={\overline{OH}}_y$ et $z=\overline{OI}$ définissaient de façon unique la position de M, les coordonnées cylindriques
$r=∥ \mathbf{OH}∥ =OH>0$,
$\theta =\left({\mathbf{e}}_x,\mathbf{OH}\right)$ de 0 à $2\pi$ et
$z=\overline{OI}$ de $-\infty$ à $+\infty$
définissent aussi de façon unique la position de M.
Si le mouvement est plan, on utilise les coordonnées polaires $\left(r,\theta \right)$.

$r=cte$ défini un cylindre de rayon $r$ (un cercle en coordonnées polaires).

$\theta =cte$ défini un demi plan perpendiculaire au plan $\left({\mathbf{e}}_x,{\mathbf{e}}_y\right)$ (une demi droite en coordonnées polaires).

$z=cte$ défini un plan parallèle au plan $\left({\mathbf{e}}_x,{\mathbf{e}}_y\right)$.

${\mathbf{e}}_r$ , ${\mathbf{e}}_{\theta }$ et ${\mathbf{e}}_z$ forment la base cylindrique (${\mathbf{e}}_r$ et ${\mathbf{e}}_{\theta }$ la base polaire) :
${\mathbf{e}}_r={\displaystyle \frac{\mathbf{OH}}{OH}}$,
${\mathbf{e}}_{\theta }$ s'obtient en tournant de $\pi /2$ dans le sens des $\theta$ croissant,
${\mathbf{e}}_z$ est le troisième vecteur de la base cartésienne.

Le vecteur position s'écrit dans la base cylindrique

$$\begin{array}{|c|}\hline \mathbf{OM}=r\hspace{0.17em}{\mathbf{e}}_r+z\hspace{0.17em}{\mathbf{e}}_z\\ \hline\end{array}$$

et dans la base polaire

$$\begin{array}{|c|}\hline \mathbf{OM}=r\hspace{0.17em}{\mathbf{e}}_r\\ \hline\end{array}$$

Relations entre paramétrage cylindrique ou polaire et paramétrage cartésien

$r=\sqrt{x^2+y^2}$	$x=\mathrm{r\; cos}\theta$
$\tan \theta ={\displaystyle \frac{y}{x}}$	$y=\mathrm{r\; sin}\theta$
${\mathbf{e}}_r=\cos \theta \hspace{0.17em}{\mathbf{e}}_x+\sin \theta \hspace{0.17em}{\mathbf{e}}_y$	${\mathbf{e}}_x=\cos \theta \hspace{0.17em}{\mathbf{e}}_r-\sin \theta \hspace{0.17em}{\mathbf{e}}_{\theta }$
${\mathbf{e}}_{\theta }=-\sin \theta \hspace{0.17em}{\mathbf{e}}_x+\cos \theta \hspace{0.17em}{\mathbf{e}}_y$	${\mathbf{e}}_y=\sin \theta \hspace{0.17em}{\mathbf{e}}_r+\cos \theta \hspace{0.17em}{\mathbf{e}}_{\theta }$

On remarque en particulier que ${\mathbf{e}}_{\theta }={\displaystyle \frac{d{\mathbf{e}}_r}{d\theta }}$ ou encore

$$\begin{array}{|c|}\hline {\displaystyle \frac{d{\mathbf{e}}_r}{dt}}={\displaystyle \frac{d{\mathbf{e}}_r}{d\theta }}{\displaystyle \frac{d\theta }{dt}}=\stackrel{.}{\theta }\hspace{0.17em}{\mathbf{e}}_{\theta }\\ \hline\end{array}$$

On pourra vérifier que

$$\begin{array}{|c|}\hline {\displaystyle \frac{d{\mathbf{e}}_{\theta }}{dt}}=-\stackrel{.}{\theta }\hspace{0.17em}{\mathbf{e}}_r\\ \hline\end{array}$$

On peut retenir la règle suivante : $\stackrel{.}{\theta }\times$ vecteur obtenu par une rotation de $\pi /2$ dans le sens des $\theta$ croissant.

Vecteur vitesse et vecteur accélération

$r$, $\theta$, $z$, mais aussi ${\mathbf{e}}_r$ et ${\mathbf{e}}_{\theta }$ dépendent du temps.

$\mathbf{v}={\displaystyle \frac{d\mathbf{OM}}{dt}}=\stackrel{.}{r}\hspace{0.17em}{\mathbf{e}}_r+r\hspace{0.17em}{\displaystyle \frac{d{\mathbf{e}}_r}{dt}}+\stackrel{.}{z}\hspace{0.17em}{\mathbf{e}}_z$

$$\begin{array}{|c|}\hline \mathbf{v}=\stackrel{.}{r}\hspace{0.17em}{\mathbf{e}}_r+r\stackrel{.}{\theta }\hspace{0.17em}{\mathbf{e}}_{\theta }+\stackrel{.}{z}\hspace{0.17em}{\mathbf{e}}_z\\ \hline\end{array}$$

$\mathbf{v}=\stackrel{.}{r}\hspace{0.17em}{\mathbf{e}}_r+r\stackrel{.}{\theta }\hspace{0.17em}{\mathbf{e}}_{\theta }$ en polaire.

Calculons le vecteur accélération :
$\mathbf{a}={\displaystyle \frac{d\mathbf{v}}{dt}}=\stackrel{..}{r}\hspace{0.17em}{\mathbf{e}}_r+\stackrel{.}{r}\hspace{0.17em}{\displaystyle \frac{d{\mathbf{e}}_r}{dt}}+\left(\stackrel{.}{r}\stackrel{.}{\theta }+r\stackrel{..}{\theta }\right)\hspace{0.17em}{\mathbf{e}}_{\theta }+r\stackrel{.}{\theta }\hspace{0.17em}{\displaystyle \frac{d{\mathbf{e}}_{\theta }}{dt}}+\stackrel{..}{z}\hspace{0.17em}{\mathbf{e}}_z$

$$\begin{array}{|c|}\hline \mathbf{a}=\left(\stackrel{..}{r}-r{\stackrel{.}{\theta }}^2\right)\hspace{0.17em}{\mathbf{e}}_r+\left(2\stackrel{.}{r}\stackrel{.}{\theta }+r\stackrel{..}{\theta }\right)\hspace{0.17em}{\mathbf{e}}_{\theta }+\stackrel{..}{z}\hspace{0.17em}{\mathbf{e}}_z\\ \hline\end{array}$$

$a_r=\stackrel{..}{r}-r{\stackrel{.}{\theta }}^2$ est la composante radiale de l'accélération.
$a_{\theta }=2\stackrel{.}{r}\stackrel{.}{\theta }+r\stackrel{..}{\theta }$ est la composante orthoradiale de l'accélération.
$a_z=\stackrel{..}{z}$ est la composante axiale.

Calculons le vecteur déplacement élémentaire :

$$\begin{array}{|c|}\hline d\mathbf{OM}=\mathbf{v}dt=dr\hspace{0.17em}{\mathbf{e}}_r+rd\theta \hspace{0.17em}{\mathbf{e}}_{\theta }+dz\hspace{0.17em}{\mathbf{e}}_z\\ \hline\end{array}$$