Repérage d'un point - Vitesse et accélération (3)

---

Les vecteurs sont notés en gras.

Coordonnées sphériques

Repérage d'un point - Vecteur position

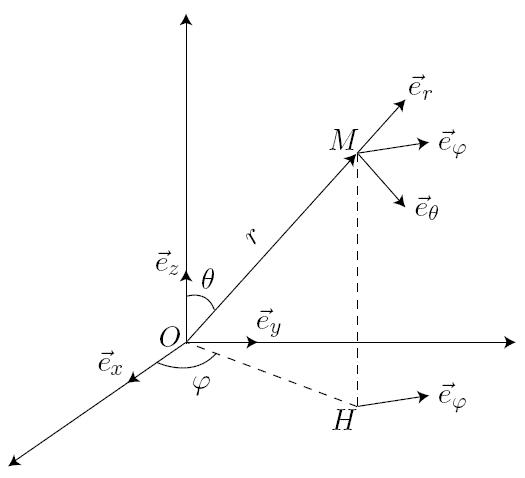
Les coordonnées sphériques $\left(r,\theta ,\varphi \right)$ définissent de manière unique la position du point M :
$r=∥ \mathbf{OM}∥$ peut varier de 0 à $+\infty$
$\theta =\left({\mathbf{e}}_z,\mathbf{OM}\right)$ peut varier de 0 à $\pi$
$\varphi =\left({\mathbf{e}}_x,\mathbf{OH}\right)$ peut varier de 0 à $2\pi$

Les vecteurs ${\mathbf{e}}_r$, ${\mathbf{e}}_{\theta }$ et ${\mathbf{e}}_{\varphi }$ constitue la base sphérique :
${\mathbf{e}}_r={\displaystyle \frac{\mathbf{OM}}{OM}}$
${\mathbf{e}}_{\varphi }$ est obtenu en tournant de $\pi /2$ dans le sens des $\varphi$ croissant à partir du vecteur $\mathbf{OH}$
${\mathbf{e}}_{\theta }={\mathbf{e}}_{\varphi }\wedge {\mathbf{e}}_r$

Le vecteur position s'écrit dans la base sphérique :

$$\begin{array}{|c|}\hline \mathbf{OM}=r\hspace{0.17em}{\mathbf{e}}_r\\ \hline\end{array}$$

Relation entre paramétrage sphérique et paramétrage cartésien (voir TD)

Vecteur vitesse et vecteur accélération (voir TD)

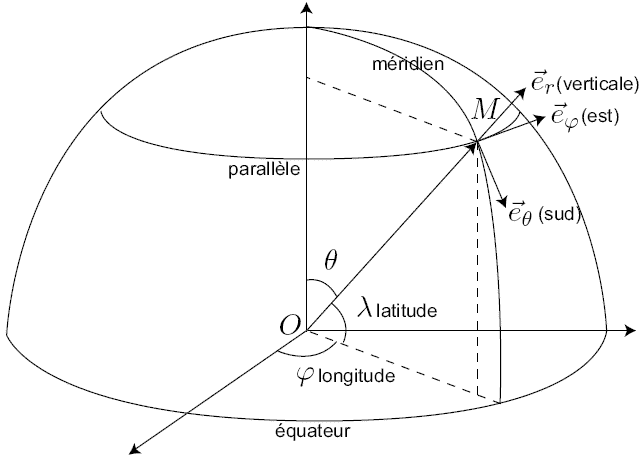
Coordonnées géographiques

Exemples de mouvement

Vecteur accélération constant

$$\mathbf{a}=\mathbf{cte}$$ $$\mathbf{v}=\mathbf{a}t+\mathbf{A}$$ $$\mathbf{OM}={\displaystyle \frac{1}{2}}\mathbf{a}{t}^2+\mathbf{A}t+\mathbf{B}$$

Mouvement rectiligne sinusoïdal

$$\mathbf{OM}=x\hspace{0.17em}{\mathbf{e}}_x\mathrm{avec}x=x_m\cos \omega t$$ $$\mathbf{v}=-x_m\omega \sin \omega t\hspace{0.17em}{\mathbf{e}}_x$$ $$\mathbf{a}=-x_m{\omega }^2\cos \omega t\hspace{0.17em}{\mathbf{e}}_x=-{\omega }^2\hspace{0.17em}\mathbf{OM}$$

Mouvement circulaire

Le paramétrage polaire est le mieux adapté :

$$\mathbf{OM}=R\hspace{0.17em}{\mathbf{e}}_r$$ $$\mathbf{v}=R\stackrel{.}{\theta }\hspace{0.17em}{\mathbf{e}}_{\theta }$$ $$\mathbf{a}=-R{\stackrel{.}{\theta }}^2\hspace{0.17em}{\mathbf{e}}_r+R\stackrel{..}{\theta }\hspace{0.17em}{\mathbf{e}}_{\theta }$$