Généralités sur la lumière

---

Du rayon lumineux à l'électrodynamique quantique

Modèle géométrique (1re année)

EUCLIDE (4e-3e avant J.-C.) notion de rayon lumineux.

ALHAZEN physicien arabe (10e-11e) attribue à la lumière une origine extérieure à l'oeil.

GALILEE (16e-17e) fabrication des premières lunettes.

DESCARTES (17e) modélisation corpusculaire de la lumière (mais impose une vitesse de la lumière plus grande dans les milieux matériels que dans l'air ce qui est en contradiction avec l'expérience).

FERMAT (17e) principe de moindre temps.

NEWTON (16e-17e) travaux considérables.

Modèle ondulatoire (2e année)

HUYGENS (17e) propose une théorie ondulatoire permettant de retrouver les résultats de l'optique géométrique et compatible avec une vitesse de la lumière plus faible dans les milieux matériels que dans l'air.

YOUNG et FRESNEL (18e-19e) la découverte des phénomènes de diffraction et d'interférences impose cette théorie.

MAXWELL (19e) la lumière comme une onde électromagnétique se propageant à une vitesse

$$\begin{array}{|c|}\hline c=3.10^8\hspace{0.17em}m.s^{-1}\\ \hline\end{array}$$

dans le vide

$$\begin{array}{|c|}\hline v={\displaystyle \frac{c}{n}}\\ \hline\end{array}$$

dans un milieu matériel où n est l'indice du milieu,

de longueur d'onde

$$\begin{array}{|c|}\hline \lambda =cT={\displaystyle \frac{c}{\nu }}\\ \hline\end{array}$$

où T est la période et $\nu$ la fréquence, la lumière visible correspondant aux longueurs d'onde

$$\begin{array}{|c|}\hline 400\hspace{0.17em}nm\left(\mathrm{violet}\right)<\lambda <800\hspace{0.17em}nm\left(\mathrm{rouge}\right)\\ \hline\end{array}$$

Modèle corpusculaire

Les découvertes de l'effet photoélectrique et du rayonnement du corps noir conduisent PLANCK et EINSTEIN à revenir à un modèle corpusculaire en introduisant les photons, particules sans masse, d'énergie

$$\begin{array}{|c|}\hline \epsilon =h\nu \\ \hline\end{array}$$

se déplaçant à la vitesse c. On parle alors de dualité onde corpuscule.

Electrodynamique quantique

Cette théorie développée entre autres par FEYNMANN dans les années 50 lève les dernières contradictions entre les aspects ondulatoire et corpusculaire.

Domaine de validité de l'optique géométrique

(D'après Pierre Léna et Alain Blanchard, Lumières une introduction aux phénomènes optiques, InterEditions 1990)

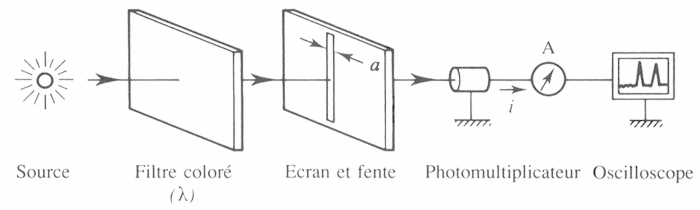
Ce dispositif met en évidence 3 quantités :
- $\nu$ fréquence (couleur);
- a largeur de la fente;
- N nombre de photons détectés par le photomultiplicateur.

Si $a\gg \lambda$ le modèle ondulatoire est inutile. Cette situation se rencontre lorsque les dimensions géométriques des obstacles que rencontre la lumière restent grandes devant sa longueur d'onde $\lambda$.
Si $N\gg 1$ le modèle du photon est inutile. Cette situation se rencontre lorsque l'on n'est pas confronté à la détection de photons un par un mais plutôt à de fortes intensités lumineuses.

Si l'on a simultanément $a\gg \lambda$ et $N\gg 1$, le modèle géométrique fait l'affaire. Dans ce cas, la lumière ne rencontre pas d'obstacles de dimensions comparables ou inférieures à sa longueur d'onde et l'énergie mise en jeu dans sa détection par le photomultiplicateur est grande devant $hc/\lambda$.

Sources de lumière

Sources à spectre continu

Un corps à la température T émet un rayonnement électromagnétique dont le spectre est continu :

La longueur d'onde ${\lambda }_m$ correspondant au maximum d'émission (du corps noir) est donnée par la loi de WIEN :

$${\lambda }_{m}T=2,987.10^{-3}\hspace{0.17em}\mathrm{K.m}$$

Exemple : ampoule classique, Soleil...

Sources à spectre de raies ou de bandes

La lumière est émise suite à la désexcitation d'atomes.

Sa décomposition par un prisme ou un réseau donne un ensemble de raies caractéristiques de la composition de la source :

$${\displaystyle \frac{\Delta \nu }{\nu }}\simeq 10^{-7}$$

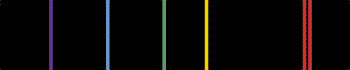
Exemples : néon, lampes spectrales utilisées en TP...

Cas particulier du LASER

(Light Amplification by Stimulated Emission of Radiation)

Le fonctionnement du LASER est basé sur le processus d'émission stimulée.

Le rayonnement émis par le LASER est quasi monochromatique :

Pour le LASER hélium néon utilisé en TP, $\lambda =632,8\hspace{0.17em}nm$ (rouge).